Por todos lados ha aparecido la noticia de un mexicano que «descubre nuevo sistema matemático» ([1], [2], [3], [4], por ejemplo), incluida la página de prensa de la Universidad de Guadalajara, donde trabaja Juan Alfredo Morales del Río, el descubridor, en el Centro Universitario de la Ciénaga.
La nota es demasiado sospechosa, sobre todo por la forma de Morales de presentar su descubrimiento. Como se describe en El Universal (las negritas son originales):
Juan Alfredo Morales, investigador del Departamento de Ciencias Tecnológicas del Centro Universitario de la Ciénega (CUCIénega) de la UdeG, oficializó hoy su descubrimiento sobre una nueva serie de números denominados trierniones.
En rueda de prensa, manifestó que caen en el campo de los hipercomplejos, compuestos de tres partes: una real y dos imaginarias, que tendrán múltiples aplicaciones, sobre todo en proyectos de inteligencia artificial.
Dijo que su hallazgo rompe con los paradigmas matemáticos, sobre todo con los tradicionales números complejos (que describe como la suma de un número real y uno imaginario), que son la herramienta de trabajo del álgebra ordinaria, llamada álgebra de los números complejos.
Esta nota tiene todos los ingredientes de la presentación por un charlatán: anuncio de un «descubrimiento» en una rueda de prensa, grandes promesas de aplicaciones por todos lados, y, desde luego, el «rompimiento de los paradigmas» actuales; la última es siempre una gran favorita.
Empecemos por el autor, que no sabemos a ciencia cierta a qué se dedica: lo mismo aparece explorando el lago de Chapala en búsqueda de pinturas rupestres, como estudiando la contaminación del río Zula o declarando que la industria mueblera de Ocotlán, Jalisco, no cumple las normas ecológicas. Tenemos dos opciones: Morales es toda una maravilla de la investigación multidisciplinaria, o nomás anda metiendo las narices en todos lados.
Rara vez se hacen anuncios de descubrimientos matemáticos (o científicos, en general) serios en rueda de prensa; lo usual es enviar el resultado a una publicación científica, arbitrada, y, una vez publicada, es la prensa especializada la que publica anuncios para el público, si la considera de interés, incluyendo entrevistas a los autores. Son pocas las excepciones en que el mismo autor hace un anuncio público; recordemos el fiasco de Lisa Wolf-Simon y su rueda de prensa, auspiciada por NASA, al anunciar su supuesta bacteria que sobrevive con arsénico.
Luego viene la afirmación que «se rompe con paradigmas», frase típica de los charlatanes para evitar muestras de escepticismo de sus interlocutores y, sobre todo, preguntas incómodas.
Pero, a final de cuentas, ninguna de mis críticas aquí expuestas es definitiva hasta no ver el trabajo anunciado. Es decir, tal vez el autor no sea matemático y, tal vez, su descubrimiento no sea la octava maravilla, pero existe la posibilidad de que su trabajo sea correcto e interesante, y nomás se dejó llevar por la emoción y la anunció como la gran promesa para la ciencia y tecnología del próximo siglo.
Los mentados trierniones
Afortunadamente la página del Centro de la Ciénaga, en su comunicado de prensa, incluye el texto del autor en versión PDF: Los números trierniones. Con una leída rápida podemos verificar que, efectivamente, el autor no es matemático y que su descubrimiento no es una maravilla. Sin embargo, tampoco es correcto, ni interesante.
Después de una introducción, formada por una no tan breve historia de los números complejos, en la segunda sección Morales define el conjunto de los trierniones (aunque los llama «serie»). Consiste de los números de la forma , donde
y
son reales y a
y
los llama «imaginarios». Más aún, forman un campo (o cuerpo, como se lee en algunas traducciones del alemán) con un par de operaciones
y
, aun por definir.
Morales escribió en el estilo de un libro de texto elemental (modelado, seguramente, de un texto de variable compleja), por lo que, por ejemplo, al enunciar su «axioma de igualdad» incluye un ejemplo, a manera de ejercicio resuelto, donde trabaja todos los detalles para concluir que, si los trierniones y
son iguales, entonces
y
. Es por eso que el PDF tiene 32 páginas, cuando unas 2 o 3 hubieran sido suficientes para decir lo mismo.
Después de explicar el «espacio hipercomplejo de los trierniones», que él llama espacio de Argand-Morales del Río (no ma…), finalmente define la suma, que no es más que la suma vectorial en . Luego gasta unas 10 páginas en verificar las propiedades de esta suma: conmutatividad, asociatividad, etc.; algunas, como la desigualdad del triángulo, solo las verifica con ejemplos.
Finalmente, en la quinta sección, define la multiplicación como
Luego se lanza, como en el caso de la suma, a verificar sus propiedades. Después de verificar el «axioma de uniformidad» con un ejemplo (donde realiza la misma multiplicación dos veces), y luego verificar conmutatividad con dos trierniones arbitrarios, verifica la asociatividad multiplicando y luego
para el caso particular
(así lo escribe),
y
.
Aquí es donde la puerca tuerce el rabo: si hubiera escogido el caso y
, entonces hubiera obtenido
y
¡que no son iguales! La operación no es asociativa; la única razón por la que funcionó con el ejemplo que él escogió es que, esencialmente, multiplicó tres veces el mismo número
, aunque multiplicado por
y
. Supongo que esa es la razón por la que no incluyó una verificación formal (tomando tres números arbitrarios): simplemente no le salió.
Curiosamente, luego de verificar en generalidad la propiedad distributiva, Morales afirma algo demasiado extraño, incluso para él: la identidad multiplicativa, el «uno triernión», es el (WTF!). No entiendo porque no le gustó, simplemente, el número 1. De hecho, es obvio que su
no es una identidad multiplicativa: si multiplican 2 por
les da
, por ejemplo, y no 2. Luego dice que
«se cumple para cualquier triernio
, exceptuando el triernión definido como triernión nulo
.» Irónicamente,
es el único para el cual se cumple dicha igualdad.
En la sección 6 Morales presenta una fórmula para la división de la cual está particularmente orgulloso:
A la ecuación (6-3) se le conocerá con el nombre de ecuación Morales del Río para la división de trierniones, ya que el ingeniero Alfredo Morales del Río la encontró al dividir un triernión entre otro usando la multiplicación por el hipercomplejo conjugado de un triernión.
Morales define el conjugado de como
, y al multiplicar estos obtiene
, un número real. De ahí que calcula la división al estilo de los complejos:
,
donde es el conjugado de
. Lo que no contaba Morales es con el hecho que, a veces, el producto de uno de sus números por su conjugado da cero, como, por ejemplo,
. Así que no podemos dividir los trierniones entre el triernión
, ¡lástima, Margarito, lástima!.
Así que el artículo de Morales, ni está correcto, ni es interesante. Más aún, al incluir demostraciones de las propiedades que sí son válidas y no incluir (ni siquiera incorrectas, como para que podamos señalar el error) las de las falsas, sugiere que, en realidad, Morales sí se dio cuenta que sus trierniones no funcionan, pero de todos modos le valió y se puso a anunciar su «descubrimiento» en rueda de prensa, quemando en el camino al rector del Centro que lo acompañó. Típica actitud de un charlatán.
¿Es posible la construcción intentada por Morales?
No. No existe un campo tridimensional (o de ninguna dimensión finita mayor a 2) que extienda al campo de los números complejos. Esto es consecuencia del teorema fundamental del álgebra: si
es un polinomio sobre los complejos de grado al menos 1, entonces tiene una raíz en
. Es decir, para cualquier polinomio
con coeficientes en
, entonces existe un número
tal que
. Más aún, esto implica que, de hecho, todas las raíces de
están en
.
Si es una extensión de, digamos, dimensión
(dimensión real), y tomamos
, entonces los números
serían linealmente dependientes (sobre
), por lo que podríamos encontrar números reales
tales que
Pero entonces es raíz del polinomio
, y concluimos que
. Por lo tanto,
(y
, desde luego).
Así que no puede existir un campo tridimensional. ¿Qué es lo mejor que podemos lograr? Recordemos que las cosas que fallan en la construcción de Morales son la asociatividad y la existencia de la división, ya que algunos números diferentes de cero pueden resultar en cero al ser multiplicados entre sí.
Un álgebra es una estructura algebraica con suma y multiplicación, tal que, mientras la suma tiene todas la propiedades de la suma en un espacio vectorial (sobre ), es decir, asociatividad, conmutatividad, elemento neutro (cero) e inversos aditivos, a la multiplicación solo le pedimos ser distributiva con la suma:
y
(tenemos que poner las dos porque no necesariamente tenemos conmutatividad).
Un álgebra de división es un álgebra sin divisores de cero, o sea, si , entonces
o
. En otras palabras, en un álgebra de división, la división es posible. En 1958, Michel Kervaire, e independientemente, Raoul Bott y John Milnor, demostraron que las álgebras de división deben tener dimensión 1, 2, 4 u 8. Así que no podemos tener divisiones en un álgebra de dimensión 3.
De hecho, si pretendemos que nuestra álgebra de división, además, sea normada (tenga valor absoluto), entonces solo hay exactamente 4 de ellas: (los reales),
(los complejos),
(los cuaterniones) y
(los octoniones), lo cual fue demostrado por Adolf Hurwitz en 1898. Cada una pierde alguna propiedad de la anterior: los complejos no están ordenados, a diferencia de los reales; los cuaterniones no tienen la propiedad conmutativa de la multiplicación, a diferencia de los complejos; y los octoniones no tienen la propiedad asociativa, a diferencia de los cuaterniones.
Para finalizar, sí es posible construir un álgebra conmutativa y asociativa de dimensión 3. Un ejemplo es el de los llamados números tricomplejos, descubiertos recientemente por Silviu Olariu, y que pueden ser vistos como una subálgebra del álgebra de matrices de .
Con esta nota participo en la edición 2.8 del carnaval de matemáticas, alojado esta vez en el blog Ciencia Conjunta.
De todas las explicaciones bien fundamentadas que he leído acerca del por qué las apreciaciones del sr. Morales son incorrectas esta ha sido la mejor; y además con un toque de humor. Felicidades.
Buena nota, Ricardo.
Que vergüenza que algo así provenga de la UdeG… aunque la UdeC le lleva ventaja, hablando de Exopolítica y demás babosadas.
Eit. Andan en todos lados.
ya por ahi lo despedazamos, estamos esperando que las autoridades hablen del ridículo, y por otro lado buena molestia que uds usaron tanto latex para tan estupida noticia.
¡Ja! No te preocupes, Juan.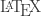 no se desgasta.
no se desgasta.
Cómo está reaccionando el Depto de Matemáticas en UdeG? Hay noticias?
Buen análisis. =P Pero te falto ver una cosa: en su «definicion» dice que $i=j$.
¡Ja, ja! Es cierto, se me pasó comentar ese detalle.
No conocía «la noticia de un mexicano que “descubre nuevo sistema matemático”, los trierniones» pero me alegra que lo hayas desmontado; siempre tiene que haber alguien que se «ensucie las manos» y lo haga. Buen trabajo. Felicidades.
Aquí en México salió en todos los periódicos a través de las agencias de noticias.
Buen articulo, sin piedad contra los charlatanes, me tome la libertad de poner el enlace a tu blog, esta nota me dejo muy indignado. Saludos.
Qué buena nota. Hay que enseñarle a este señor que no puede meterse con la Ciencia y salir triunfante. Debe ser cuestión de tiempo para que lo despidan.
Hacía el final, tu empleo de la palabra «dimensión» se vuelve ambiguo. En todo caso, te recomendaría cambiar «No existe un campo tridimensional (o de ninguna dimensión finita mayor a 2) que extienda al campo de los números complejos» por «No existe una extensión de campos sobre los números reales de grado finito mayor a 2», y «Para finalizar, sí es posible construir un álgebra conmutativa y asociativa de dimensión 3.» por «Para finalizar, sí es posible construir un $\mathbb{R}$-álgebra conmutativa y asociativa de dimensión 3.» Hay que notar también que la observación de Rodrigo Hernandez Gutierrez invalida tu prueba.
Buen post, saludos.
La tercera parte es más técnica y tuve que dejarla, como dices, más ambigua. Escribirla con total formalidad hubiera hecho el post demasiado largo, y se hubiera perdido el objetivo original.
Hola Ricardo. Se te pasó mencionar que este señor empieza suponiendo que lo que va a construir (sin pensar en cuantas reputaciones iba a destruir) es un campo, y escribe los axiomas de estos, a los que llama leyes. Pareciera que maquavélicante ahi da la versión Morales de Río de la asociatividad de producto (que muchas páginas después, asumiendo la demencia de sus lectores, substituye por el axioma común)
x(yz)= xy+xz
el cual lleva a contradicciones inmediatas. Aunque si lo que quería era de verdad construir un campo, trató de esconder (sin mucho éxito) que i=j……
Saludos,
El Departamento de Matemáticas no avala ni ha avalado los resultados presentados por el Sr. Juan Alfredo Morales del Río acerca de sus TRIERNIONES ya que estos no muestran la consistencia ni la formalidad requerida para ser considerados como un trabajo científico y además presentan serias inconsistencias en su formulación.
Atentamente
Dr. Miguel Angel Olmos Gómez
Jefe del Departamento de Matematicas
División de Ciencias Básicas
Centro Universitario de Ciencias Exactas e Ingenierías
Universidad de Guadalajara
la pregunta es ¿como se filtro el trabajo de morales hasta la prensa y el publico sin antes haber pasado por el departamente de matematicas?, esto es muy curioso
Puliendo un poco mi comentario: tu respuesta es excelente en el sentido que describe todas las posibles «interpretaciones» de ese sinsentido,
pero siendo m’as espec’ificos, este sen~or define su producto como una simple extensi’on lineal en los generadores 1, i,j, y por lo tanto es conmutativo y asociativo, por definici’on!!!! Me pregunto si torci’o el axioma de la asociatividad a prop’osito al final como patadas de ahogado, pues es precisamente la asociatividad del producto la que implica que i=j.
Hola Claudio. El objetivo del post fue comentar la nota de forma entretenida (quise divertirme al escribirlo), y por eso me fui comentando algunos detalles del artículo, aunque se contradicen unos a otros.
No creo que Morales haya intentado «torcer» axiomas; en realidad, creo que no tiene la menor idea de lo que escribió, y se puso a anunciar con bombo y platillo un «descubrimiento» que imaginó tener.
chupame un huevo de seguro eres un idota que no sbes trabajar por eso te dedicas demasiado a las mierdas de la matematica que no sirven para nada
¡Ja, ja! No ma…
Jajajajajajaja…. de todos los posts, este fue el mas gracioso!!
Deberíamos llamar a El Universal para que lo publiquen!!! jajajaja
Aparentemente el Sr Morales del Rio también lee este blog.
y miren, aquí la muestra de la ignorancia…
Jajajaja me encanto, aun no paro de reírme. Ese Morales se cebó.
¿ como es eso de que entonces x = 5 4=3 y z=3? no manchen entonces yo y el papa somos el mismo, ja ja ja
¡Ja, ja! El « » fue un error de dedo mío. Gracias por avisar; ya está corregido.
» fue un error de dedo mío. Gracias por avisar; ya está corregido.
Hay no pobre tipo, no esta ni capacitado para dar clases a wachiturnos de secundaria, cuanta barbarie, no no no no.
Como critican el trabajo de un mexicano que se esfuerza por hacer algo para la superacion del pais mientras ustedes bola de pendejos lo unico que saben es criticar y hablar en vez de ayudarlo si se equivoco en algo para que mexico progrese, ponganse a enfocar todas sus criticas y si son tan chingones hagan algo mejor en sus putas y enfadosas matematicas a ver si es cierto que muy habladores ricardos me cae que ni en 1 siglo sales en algun periodico, a lo mejor lo unico que sabes hacer es ver revistas de tv y novelas no que muy chingon, has algo por el pais y ya callate la boca como se nota que eres mexicano por que asi es el perfil de nosotros nada que ver con los chinos que se ayudan y son bien fregones, aqui en mexico si alguien quiere sobresalir lo muerden de los pies y no se logra nada…. no demuestres que eres muy chingon con palabras por que se las lleva el viento muestralo con hechos la integral de 23285 sigueme chupando un huevo y que pendejo te ves mas idiota tu jajajajaja Sr. Jose Alfredo Morales Muchas felicidades por hacer algo productivo y no dedicarse a criticar el trabajo de otros al menos tiene algo interezante que hacer no como el pendejo de Ricardos….
Otro mongol, criticamos el trabajo porque es una redundancia y una redundancia mal hecha, esta persona solo quiere salir en los medios de comunicación, porque obviamente no tiene la minina idea de lo que es la investigación científica por lo menos en México y mucho menos en las matemáticas. Desde luego que en México hay importantes resultados en varias ramas como la topología de continuos y el álgebra abstracta, y no por eso los autores andan haciendo lo que este tipejo hace. Como diría el Dr. Roberto Martínez Villa: «En los albores de la matemática, lo que al hombre neandertal se le ocurrió después de haber descubierto el uuuno… fue el dooosss (¿y luego que?) y luego el treeeees…. » eso es lo que quiso inventar este tipejo, pero en este caso para su sorpresa no hay «treeess….» por que es la misma cosa que el «dooosss…» y si existiese tal «treeess….» el álgebra se viene abajo por que contradice su teorema fundamental el cual es bastante serio en comparación con esta mafufada del Sr. Morales.
Se me hace que tu puta mdres es Pedro Zepeda el cual comentó la nota que aparecida en el sitio de la UdeG http://www.udg.mx/node/20385#disqus_thread porque es de los pocos que felicita a Morales alli y menciona a los chinos asi como lo hace aqui.
¡Qué onda contigo! ni siquiera tienes un ‘nick’ a la altura de este blog, y se nota mucho que ni tú ni el Sr. Morales tienen idea de lo que es hacer investigación en serio. Para tu información, Ricardo estuvo en la Universidad de Princeton, el mismo lugar donde estudió John Nash (tal vez es demasiada información para ti). Y así muchos de nosotros de alguna u otra forma nos destacamos, por lo que es realmente triste leer que saltan pendejos a defender otros pendejos (no se les puede llamar de otra forma) cuando se les refuta información contradictoria que publican en medios no especializados, con el clásico argumento de los «cangrejos mexicanos»; aquí simplemente no aplica. Antes de opinar, por favor instrúyete aunque sea lo mínimo en la materia.
Simplemente no se puede aplaudir un trabajo que tiene todas esas inconsistencias, no le hacemos ningún bien. Ojala que el ingeniero Morales tome todas estas criticas a su favor, y que se anime a trabajar en equipo con investigadores de la ciencia matemática. Es en colaboración como se avanza. (Y si, los chinos tienen lo suyo… para bien y para mal)
Distiguido Sr. «Puta Madres» (no me proporciona usted alguna referencia o algo que me indique como dirigirme a usted, asi que utilizare lo que parece ser su apellido): Le respondere por 2 razones: 1) Estoy aburrido 2) creo que su preocupacion acerca de «los mexicanos envidiosos destrozando el trabajo de otros mexicanos» es genuina (probablemente no lo es, pero partire de ese supuesto):
En primer lugar quiero aclarar que no defiendo al administrador del blog, evidentemente no necesita que se le defienda, y aunque puedo entender su frustracion, porque efectivamente es frecuente en nuestra cultura despedazar a quien comete la osadia de triunfar donde otros fracasan, este no es el caso, es lo que aclara el post, mi preocupacion es que ese nacionalismo mal entendido hace tanto daño como el otro extremo que usted menciona, puede usar el lenguaje que usted desee, el hecho es que si algo esta mal fundamentado, dentro de una disciplina tan rigurosa como las matematicas lo está sin importar si esto lo formuló el investigador mas reputado o un alumno de preparatoria, esa es la belleza de la ciencia, no pesa la autoridad ni la reputacion del investigador mas que la validez de sus teorias, lo opuesto es el dogma, que bien que le preocupe el bienestar de mexico, lea con atención, trabaje en su campo de especialidad y le aclaro que no soy matematico, sí me sé ganar la vida con trabajo manual (cosa aparentemente indispensable para que mis opiniones tengan validez) pero con su ataque hace precisamente lo que critíca: destruir el trabajo de quien se dedica a la investigacion.
Señor «tu puta madres», si de verdad tienes admiración por los chinos deberías pedir que ejecuten al Sr. Morales, debido a la vergüenza internacional a la que ha metido a México; deberías pedir a la prensa que informó de este fiasco que limpien su nombre publicando disculpas tras disculpas; etc… si este blog desmiente a las pocas personas que lo leen es porque es un oasis en medio del estiércol. Las matemáticas son un paraíso que ni el sr. Morales ni nadie podrá corromper. Definitivamente nuestro peor enemigo es la estupidez.
De risa loca una frase en las conclusiones de Morales del Río acerca de la exhaustiva búsqueda de «números complejos que se encontrasen en la tercera dimensión en toda la historia de las matemáticas». Como se puede «constatar», esa búsqueda consistió en dos libros de divulgación de la historia de las matemáticas, uno propiamente de «historia de las matemáticas» y otro de «historia general de las ciencias». ¿No consultó las obras originales de tantos matemáticos que trataron de algún modo la variable compleja?
Los genios no necesitan de esas trivialidades, reconstruyo las obras originales a partir de las notas en esos libros.
Se dice ‘no es correcta’ y no ‘no está correcta’
Tienes razón; ya está corregido. Gracias.
Ricardo, tal vez el Sr. Morales se hubiera metido en menos problemas si mencionara que sus «trierniones» son un subgrupo de los cuaterniones bajo la suma, pero lo más grave es que su multiplicación fue todo un desastre. A todo esto, ¿siquiera es Dr. ese señor? … aunque no lo avalen, ya se quemó muy feo la UdeG. IMuchos saludos!
Es Maestro en Ciencias (quién sabe en qué), no es Doctor.
Pues no se cual es el trabajo de «Silviu Olaru» pero encontrar un algebra de dimension 3 que sea asociativa y comutativa me parece que no es de gran cosa. Solo toma el «group algebra» the un grupo de orden 3. De igual manera puedes hacer![\mathbb{R}[\frac{\mathbb{Z}}{n\mathbb{Z}}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BR%7D%5B%5Cfrac%7B%5Cmathbb%7BZ%7D%7D%7Bn%5Cmathbb%7BZ%7D%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002)
Ah! no me funciono el LaTex :(
Bueno agarra el grupo ciclico de n elementos y toma su «group algebra » e voila.
Ya corregí tu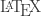 . Tienes que escribir la palabra «latex» justo después del $, y luego el código.
. Tienes que escribir la palabra «latex» justo después del $, y luego el código.
En este manuscrito en ArXiV Silviu Olariu introdujo su versión tridimensional de los complejos: Complex numbers in three dimensions. La gracia de estos números es que puedes definir versiones análogas de analiticidad, integrales de línea, etc., y tienes resultados análogos a los clásicos de la variable compleja.
Ooooorales…. este señor también es antropólogo
http://www.informador.com.mx/cultura/2009/91785/6/en-peligro-los-petroglifos-de-la-ribera-de-chapala.htm
Buen trabajo ricardos.
Cuando leí la «noticia» hace una semana… reventé.
Pensé: ¿Se le pasaron a Hamilton por allá de los 1800?
Y consideré descubrir los pentaniones antes de que alguien me los ganara.
Magnífico trabajo de investigación y comprobación. De acuerdo con este planteamiento, Morales está, entonces, llegando a un punto cercano a la ficción. Si no es real la propuesta, entonces, ¿cuál es la intención del autor del supuesto descubrimiento?
Al autor.
No me tom´´e la molestia de leer el trabajo de Morales, aunuqe si v´´i su noticia. SIn embargo si le´´i el tuyo y tu demostraci´´on de que F=C tiene la tremenda falla de que si los {alpha^^n} son linealmente independientes entonces los {a_n} son todos iguales a cero, lo que vuelve a tu polinomio el polinomio id´´enticamente cero(el cual manda a todos los triernios al cero). As´´i , no puedes concluir que alpha sea complejo, ni que F=C
Hola, Ax: Los números no pueden ser independientes porque son más que la dimensión (asumida igual a
no pueden ser independientes porque son más que la dimensión (asumida igual a 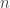 ). Así que deben ser dependientes y de ahí es donde uno concluye que
). Así que deben ser dependientes y de ahí es donde uno concluye que 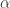 es raíz de un polinomio de grado a lo más
es raíz de un polinomio de grado a lo más 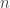 .
.
Respondo a la respuesta de ricardos aquí porque en su comentario no me da la opción de responder. Ahí hay un error de dedo, las potencias de alpha son l.d. sobre C, no sobre R. Por supuesto eso no altera el resto de la prueba.
Hola, Rafael: Son linealmente dependientes sobre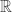 porque la hipótesis es sobre la dimensión real, o sea, sobre
porque la hipótesis es sobre la dimensión real, o sea, sobre 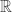 .
.
ah, ya entendí, tienes razón. Saludos.
Para llorar:
[audio src="http://www.prensaycomunicaciones.udg.mx/hsldocs/cmscalendar/cmscalendar_1816-audio-RP%20Hallazgo%20matematico_17Nov.mp3" /]
Sólo le pido un mínino de respeto para hacer matemáticas.
Para llorar, pero de risa. ¡Ja, ja! No había escuchado el audio y está bien cotorro, ¡juar, juar!
Por cierto, ¿de dónde habrá sacado Morales que Adolfo le dijo que «hay que mostrar tu resultado al mundo»? No mamen. Nomás quemando gente que no tiene nada qué ver. (Al menos que Morales se haya creído un sarcasmo.)
Del enojo a la pena en una semana…
Sí se publicó el «artículo» :S http://cuci.udg.mx/INVESTIGACION/index.php/publicaciones
y la revista está en Latindex :S
http://www.latindex.org/buscador/ficRev.html?folio=20768&opcion=1
Obvio se tiene que hacer algo para no afectar a los demás investigadores publicados en la revista. :( Pus que no hay revisores?
Chales…! que quemada para la revista…..
Y va de mal en peor: http://gerardo1313.wordpress.com/2011/11/24/numeros-imaginarios-numeros-magicos/
http://www.academica.mx/categorias/etiquetas-observatorio/numeros-trierniones
Le estoy dando seguimiento a la noticia sólo esperando a que en alguno de los medios que dieron la noticia se desmienta el fraude… ¿no se han enterado? ¿Los reporteros no dan seguimiento a las noticias que reportan? ¿les dará pena rectificar y admitir que fueron víctimas de un charlatán? ¿Tampoco el centro de estudios que auspició a Morales dirá nada?
A parte de los aspectos propiamente matemáticos que ya Ricardos se ha encargado de apuntar, a parte de que la misma rueda de prensa delata casi por sí misma el fiasco que se expone (escuchar el audio), sorprende el hecho de que el mismo artículo de Morales del Río carece de todo rigor académico, no digamos matemático, para acabar, la redacción es propia de alguien que no tiene idea (pero cree tenerla) de lo que está hablando y el contexto en el que se escriben los artículos académicos y de investigación.
«Un álgebra es una estructura algebraica con suma y multiplicación» suena un poco redundante, yo más bien diría que un álgebra es una estructura que consta de un conjunto de elementos (números reales, o complejos, por ejemplo), junto con dos operaciones, suma y resta, que operan sobre esos elementos.
perdón quise decir suma y multiplicación en lugar de suma y resta
Hola Daniel: Claro, suena redundante. Es el problema de que en el álgebra se estudien álgebras. Saludos.
Puedes darle click al link de la definición que publicó ricardos para que te lleve a una explicación más detallada de lo que es un álgebra.
Del Director de CIMAT:
http://www.cronica.com.mx/notaOpinion.php?id_nota=619738
Adolfo Sánchez Valenzuela sale a desmentir las calumnias de Morales del Río: https://fisica.ugto.mx/~selimibn/wp-content/uploads/2011/11/EvaluacionTrierniones.pdf
Por eso no hay que morderse la lengua, le hubiera dicho que estaba tonto y Morales no habría usado su nombre. Y aquí la página de un señor que se tomó la noticia en serio y ahora no quiere reconocer que la surró: http://gerardo1313.wordpress.com/2011/11/30/matematicos-rabiosos-primo-levi-y-otras-discusiones/
efrain, apenas hoy encontre el documento EvaluacionTrierniones.pdf. Sabes si hay manera de «verificar» la autenticidad del mismo?
Por otro lado, el documento me deja unas cuantas incomodidades. Si es el álgebra con generadores
es el álgebra con generadores  y producto
y producto  extendido linealmente, no me parece que pueda ser isomorfa a
extendido linealmente, no me parece que pueda ser isomorfa a  , pues ambos sumandos directos en la última son álgebras asociativas y
, pues ambos sumandos directos en la última son álgebras asociativas y  no lo es. De hecho, siendo
no lo es. De hecho, siendo  no asociativa, no veo cuál sería una definición razonable de ideal (y por lo tanto de álgebra simple) que se reduzca a la definión de ideal cuando el álgebra no asociativa es de Lie, digamos.
no asociativa, no veo cuál sería una definición razonable de ideal (y por lo tanto de álgebra simple) que se reduzca a la definión de ideal cuando el álgebra no asociativa es de Lie, digamos.
Por otro lado, el mapeo (digamos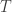 ) que se indica enviando
) que se indica enviando 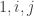 a
a  respectivamoente no es un morfismo de álgebras. Pues
respectivamoente no es un morfismo de álgebras. Pues  y
y  .
.
¿Qué opinan? Espero salga bien el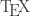 .
.
Hola Rafael: Un ideal derecho (ó izquierdo) de un álgebra es un subespacio
es un subespacio  tal que
tal que  . Un álgebra es simple si la multiplicación no es trivial y no tiene ideales propios. Algunos libros definen la suma directa de dos álgebras de Lie
. Un álgebra es simple si la multiplicación no es trivial y no tiene ideales propios. Algunos libros definen la suma directa de dos álgebras de Lie  tomando la suma directa de espacios vectoriales y después declarando a estas dos como ideales que conmutan entre si, es decir,
tomando la suma directa de espacios vectoriales y después declarando a estas dos como ideales que conmutan entre si, es decir, ![[\mathfrak{g}_{1},\mathfrak{g}_{2}]=0](https://s0.wp.com/latex.php?latex=%5B%5Cmathfrak%7Bg%7D_%7B1%7D%2C%5Cmathfrak%7Bg%7D_%7B2%7D%5D%3D0&bg=ffffff&fg=333333&s=0&c=20201002) . Supongo que en este caso sería mejor usar el término «extensión central» de
. Supongo que en este caso sería mejor usar el término «extensión central» de 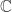 que «suma directa».
que «suma directa».
Por cierto, el isomorfismo no está bien escrito: en realidad está dado así:



Saludos
Y CRECE LA BOLA DE NIEVE: http://anuario.upn.mx/index.php/noticias-educativas/2011/630-el-informador/49516-investigador-de-la-udeg-descubre-nuevo-sistema-matematico.html
LA VÍCTIMA: UNIVERSIDAD pedagógica NACIONAL
Al menos un periódico le hizo caso a Juan Antonio Pérez, de Zacatecas, que dio una plática para cotorrear sobre el asunto: Expone profesor de la UAZ «falsedad» de un nuevo sistema númerico.
Vean (escuchen más bien) ahora ésto:
http://www.ivoox.com/el-explicador-2011-12-02-incompletitud-godel-numeros-trierniones-audios-mp3_rf_925415_1.html
Más material para reír un rato, y luego preocuparse por la situación en que se encuentra la divulgación de las matemáticas en nuestro país.
¡’Uta! Tache para Ganem: si se hubiera tomado la molestia de buscar «Alfredo Morales del Río» en Google, mínimo se hubiera encontrado con este blog, aunque también con la carta de Claudio, la respuesta de José Antonio, o el desmentido de Adolfo. Todo eso estaba disponible antes del 2 de diciembre, la fecha del programa.
Pero no es tanto la divulgación de las matemáticas, sino es la divulgación de la ciencia en el país.
¿Tache nada más para Ganem??? Oye Ricardo, se ve que ya no quieres que te cuenten entre los «matemáticos rabiosos». Viendo la lista de temas de los que se ocupa «el explicador», me parece que se le aplica lo mismo que dijiste de Morales «o es toda una maravilla de la investigación multidisciplinaria, o nomás anda metiendo las narices en todos lados».
Ya hasta le encontró aplicaciones a los trierniones que ni el mismo Morales se había imaginado.
Ya pusieron en la página de ivoox el audio del programa de ayer, y no encontré aclaración al respecto. ¿De verdad ningún colega le habrá escrito? Por lo pronto yo ya le mandé email, a ver que pasa.
OK, pues, que chingue su madre Ganem.
De hecho, está peor el programa del lunes 28, donde dijo que iba a preguntar a sus «conocidos matemáticos» sobre el asunto antes de comentar la nota. Obviamente no lo hizo: El explicador: 28 de noviembre.
Por cierto que se avienta toda una defensa de la UAG (¿¡!?) creyendo que Morales del Río trabaja ahí.
Excelente nota. Había leído la publicación en el Universal y en verdad me hizo decir en voz alta un «¡no mames!», si bien el Álgebra no es mi campo de estudio, he llegado a asistir a cursos de Teoría de Galois y sé un poquito de Teoría de Campos. En verdad me parecío una charlatanería, como esas pomadas de veneno de abeja que hasta curan el SIDA. De todos modos fui muy holgazán para verificarlo por mi cuenta,muchas gracias por dar a conocer esto.
Estudio el doctorado y veo compañeros que son prospectos para futuros Morales del Rio. Estoy seguro que ya hay muchos de esos (ya graduados) regados por el mundo, pero se quedan en las sombras debido a que sus mismos colegas los han vetado, y con justa razón. El problema es no darse cuenta a tiempo y dejarlos publicar sus controvertidos trabajos, y dejarse arrastrar por el ridículo. Algunos tienen exito en eventos sociales, y en hacer lo que les queda mejor: alardear sobre sus logros profesionales. ¡Nomás que no publiquen!
Alain
este señor Juan Alfredo Morales del Río es mi profesor de física aplicada en la materia de »mecánica» en el Centro Universitario de la Ciénega. Créanme es un excelente maestro, con un muy buen desempeño en su materia, llevándome al lado de los números triernios denominados »hipercomplejos» asistí por un breve momento a la conferencia que se llevo a cabo en la biblioteca del centro universitario en la cual explicó su trabajo de investigación científica y de lo que se trataba todo esto, pero a decir verdad no se yo sus argumentos, ni en que se baso para su investigación y »descubrimiento» de estos números, y sinceramente no se que opinar debido a que esto a causado de cierta manera una polémica dentro de la comunidad de científicos y matemáticos debido a que ya existían desde hace mucho tiempo investigaciones ya realizadas sobre el tema, por otros científicos.
Ingeniero tenia que ser, lamentablemente, es feo el tener que ver como algo que creyó haber construido se desploma tan fácil con el teorema fundamental…